Gaussian Mixture Models
Contents
11.2. Gaussian Mixture Models¶
The Gaussian Mixture Models (GMM) can be viewed as an extension of K-means. Instead of using a hard clustering method to assign each data point to one and only one cluster, the Gaussian Mixture Models estimates the probability of a data point coming from each cluster.
11.2.1. Mathematics¶
Suppose that we have \(N\) observations with \(D\) dimensions. The model is a mixture of \(K\) different Gaussian distributions, each with its own mean \(\boldsymbol{\mu}_k\) and variance \(\boldsymbol{\Sigma}_k\) such that within each cluster, the probability of observing \(\boldsymbol{x}_i\) is
We define a latent variable \(\boldsymbol{z}=(z_{1},z_{2},\dots z_{K})\), where \(z_{k}\) is 1 if a data point of interest comes from Gaussian \(k\), and 0 otherwise. Now the overall probability of observing a point that comes from Gaussian \(k\) is
Thus, each Gaussian in the model will have the following parameters: \(\pi_k\), \(\boldsymbol{\mu}_k\), \(\boldsymbol{\Sigma}_k\).
11.2.2. Expectation - Maximization Algorithm (EM)¶
Initialize \(\theta=(\pi_k, \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)\) randomly
Alternate:
E-step: based on \(\theta\), calculate the expectation of log-likelihood and estimate \(\gamma(z_{ik})\), the poterior probability that observation \(\boldsymbol{x}_i\) comes from Gaussian \(k\)
M-step: update \(\theta\) by maximizing the expectation of log-likelihood based on \(\gamma(z_{ik})\)
When the algorithm converges or when
iter = max_iter, terminate.
For more details about mathematics and the EM algorithm: https://towardsdatascience.com/gaussian-mixture-models-explained-6986aaf5a95, https://towardsdatascience.com/gaussian-mixture-models-vs-k-means-which-one-to-choose-62f2736025f0.
11.2.3. Implementation¶
GMM can also be implemented by importing the scikit-learn package.
11.2.4. Iris data¶
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
iris_data = datasets.load_iris()
iris = pd.DataFrame(iris_data.data,columns=["sepal_length","sepal_width","petal_length","petal_width"])
iris['species'] = pd.Series(iris_data.target)
iris.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 150 entries, 0 to 149
Data columns (total 5 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 sepal_length 150 non-null float64
1 sepal_width 150 non-null float64
2 petal_length 150 non-null float64
3 petal_width 150 non-null float64
4 species 150 non-null int64
dtypes: float64(4), int64(1)
memory usage: 6.0 KB
sns.FacetGrid(iris,hue="species", height=3).map(sns.histplot,"petal_length").add_legend()
sns.FacetGrid(iris,hue="species", height=3).map(sns.histplot,"petal_width").add_legend()
sns.FacetGrid(iris,hue="species", height=3).map(sns.histplot,"sepal_length").add_legend()
plt.show()
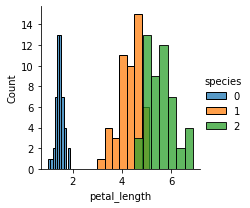
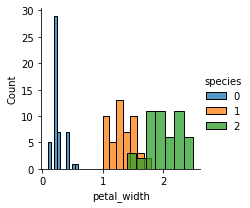
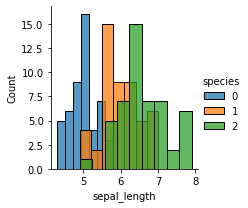
For a more concise visualization later, we just select sepal_length and sepal_width as the input variables.
X = iris.iloc[:, [0, 1]].values
y = iris.iloc[:, 4]
11.2.4.1. Training GMM¶
from sklearn.mixture import GaussianMixture
GMM = GaussianMixture(n_components = 3)
GMM.fit(X)
GaussianMixture(n_components=3)
11.2.4.2. Results¶
We can plot the Gaussians by using a plot_gmm function defined on
https://jakevdp.github.io/PythonDataScienceHandbook/05.12-gaussian-mixtures.html.
from matplotlib.patches import Ellipse
def draw_ellipse(position, covariance, ax=None, **kwargs):
"""Draw an ellipse with a given position and covariance"""
ax = ax or plt.gca()
# Convert covariance to principal axes
if covariance.shape == (2, 2):
U, s, Vt = np.linalg.svd(covariance)
angle = np.degrees(np.arctan2(U[1, 0], U[0, 0]))
width, height = 2 * np.sqrt(s)
else:
angle = 0
width, height = 2 * np.sqrt(covariance)
# Draw the Ellipse
for nsig in range(1, 4):
ax.add_patch(Ellipse(position, nsig * width, nsig * height,
angle, **kwargs))
def plot_gmm(gmm, X, label=True, ax=None):
ax = ax or plt.gca()
labels = gmm.predict(X)
if label:
ax.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis', zorder=2)
else:
ax.scatter(X[:, 0], X[:, 1], s=40, zorder=2)
ax.axis('equal')
w_factor = 0.2 / gmm.weights_.max()
for pos, covar, w in zip(gmm.means_, gmm.covariances_, gmm.weights_):
draw_ellipse(pos, covar, alpha=w * w_factor)
plot_gmm(GMM, X)
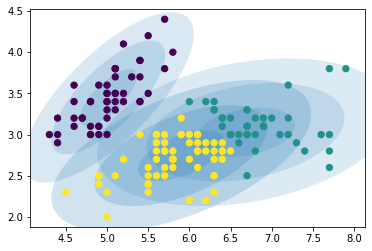
# print the converged log-likelihood value
print(GMM.lower_bound_)
# print the number of iterations needed
# for the log-likelihood value to converge
print(GMM.n_iter_)
-1.4987505566235162
8
11.2.4.3. Prediction¶
If we have some new data, we can use GMM.predict to predict which Gaussian they belong to.
from numpy.random import choice
from numpy.random import multivariate_normal
# first choose the clusters for 4 new data points
draw = choice(range(3), 4, p=GMM.weights_)
# sample the new data points within their chosen cluster
sample_test=[]
for i in range(len(draw)):
n = draw[i]
sample_test.append(
multivariate_normal(GMM.means_[n],GMM.covariances_[n]))
GMM.predict(sample_test)
array([1, 1, 0, 1])
11.2.5. Comparison to K-means¶
Both GMM and K-means are unsupervised clustering models, but GMM seems to be more robust as it introduces probabilities. However, GMM is generally slower than K-Means because it takes more iterations to converge. GMM can also quickly converge to a local minimum, not the optimal solution.
In practice, GMM can be initialized by K-Means centroids to speed up the convergence.