Contents

Linear and Generalized Linear Models

9.3. Linear and Generalized Linear Models

Let’s simulate some data for illustrations.

import numpy as np
import statsmodels.api as sm

nobs = 200
ncov = 5
np.random.seed(123)
x = np.random.random((nobs, ncov)) # Uniform over [0, 1)
beta = np.repeat(1, ncov)
y = 2 + np.dot(x, beta) + np.random.normal(size = nobs)

y.shape

(200,)

x.shape

(200, 5)

That is, the true linear regression model is

\[y = 2 + x_1 + x_2 + x_3 + x_4 + x_5 + \epsilon.\]

A regression model for the observed data can be fitted as

xmat = sm.add_constant(x)
mymod = sm.OLS(y, xmat)
myfit = mymod.fit()
myfit.summary()
OLS Regression Results
Dep. Variable: y R-squared: 0.309
Model: OLS Adj. R-squared: 0.292
Method: Least Squares F-statistic: 17.38
Date: Fri, 29 Jul 2022 Prob (F-statistic): 3.31e-14
Time: 22:52:58 Log-Likelihood: -272.91
No. Observations: 200 AIC: 557.8
Df Residuals: 194 BIC: 577.6
Df Model: 5
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
const 1.8754 0.282 6.656 0.000 1.320 2.431
x1 1.1703 0.248 4.723 0.000 0.682 1.659
x2 0.8988 0.235 3.825 0.000 0.435 1.362
x3 0.9784 0.238 4.114 0.000 0.509 1.448
x4 1.3418 0.250 5.367 0.000 0.849 1.835
x5 0.6027 0.239 2.519 0.013 0.131 1.075
Omnibus: 0.810 Durbin-Watson: 1.978
Prob(Omnibus): 0.667 Jarque-Bera (JB): 0.903
Skew: -0.144 Prob(JB): 0.637
Kurtosis: 2.839 Cond. No. 8.31


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

How are the regression coefficients interpreted? Intercept?

Why does it make sense to center the covariates?

Now we form a data frame with the variables

import pandas as pd
df = np.concatenate((y.reshape((nobs, 1)), x), axis = 1)
df = pd.DataFrame(data = df,
                  columns = ["y"] + ["x" + str(i) for i in range(1,
                  ncov + 1)])
df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 200 entries, 0 to 199
Data columns (total 6 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   y       200 non-null    float64
 1   x1      200 non-null    float64
 2   x2      200 non-null    float64
 3   x3      200 non-null    float64
 4   x4      200 non-null    float64
 5   x5      200 non-null    float64
dtypes: float64(6)
memory usage: 9.5 KB

Let’s use a formula to specify the regression model as in R, and fit a robust linear model (rlm) instead of OLS.

import statsmodels.formula.api as smf
mymod = smf.rlm(formula = "y ~ x1 + x2 + x3 + x4 + x5", data = df)
myfit = mymod.fit()
myfit.summary()
Robust linear Model Regression Results
Dep. Variable: y No. Observations: 200
Model: RLM Df Residuals: 194
Method: IRLS Df Model: 5
Norm: HuberT
Scale Est.: mad
Cov Type: H1
Date: Fri, 29 Jul 2022
Time: 22:52:58
No. Iterations: 16
coef std err z P>|z| [0.025 0.975]
Intercept 1.8353 0.294 6.246 0.000 1.259 2.411
x1 1.1254 0.258 4.355 0.000 0.619 1.632
x2 0.9664 0.245 3.944 0.000 0.486 1.447
x3 0.9995 0.248 4.029 0.000 0.513 1.486
x4 1.3275 0.261 5.091 0.000 0.816 1.839
x5 0.6768 0.250 2.712 0.007 0.188 1.166


If the model instance has been used for another fit with different fit parameters, then the fit options might not be the correct ones anymore .

For model diagnostics, one can check residual plots.

import matplotlib.pyplot as plt

myOlsFit = smf.ols(formula = "y ~ x1 + x2 + x3 + x4 + x5", data = df).fit()
fig = plt.figure(figsize = (12, 8))
## residual versus x1; can do the same for other covariates
fig = sm.graphics.plot_regress_exog(myOlsFit, 'x1', fig=fig)

eval_env: 1
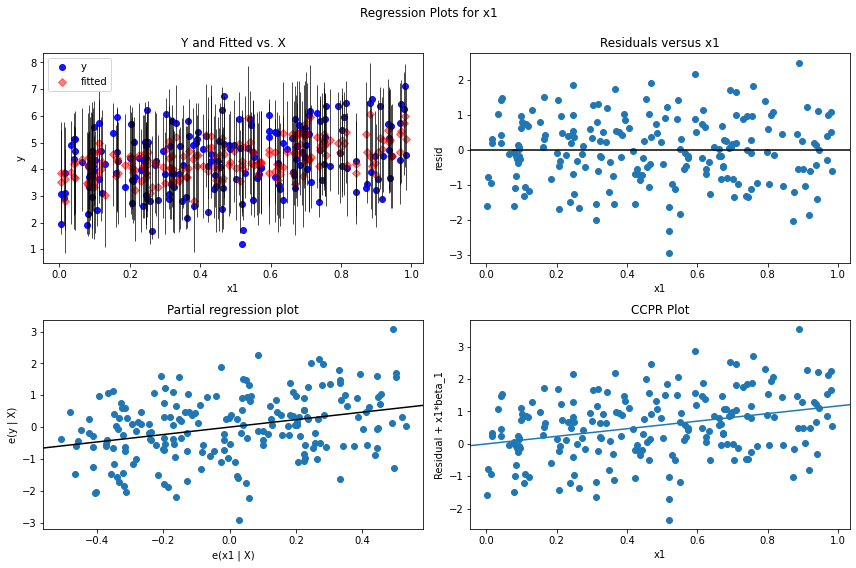
../_images/models_11_1.png

See more on residual diagnostics and specification tests.

9.4. Generalized Linear Regression

A linear regression model cannot be applied to presence/absence or count data.

Binary or count data need to be modeled under a generlized framework. Consider a binary or count variable \(Y\) with possible covariates \(X\). A generalized model describes a transformation \(g\) of the conditional mean \(E[Y | X]\) by a linear predictor \(X^{\top}\beta\). That is

\[\begin{equation*} g( E[Y | X] ) = X^{\top} \beta. \end{equation*}\]

The transformation \(g\) is known as the link function.

For logistic regression with binary outcomes, the link function is the logit function

\[\begin{equation*} g(u) = \log \frac{u}{1 - u}, \quad u \in (0, 1). \end{equation*}\]

What is the interpretation of the regression coefficients in a logistic regression? Intercept?

A logistic regression can be fit with statsmodels.api.glm.

Let’s generate some binary data first by dichotomizing existing variables.

df['yb' ] = np.where(df['y' ] > 2.5, 1, 0)
df['x1b'] = np.where(df['x1'] > 0.5, 1, 0)

Fit a logistic regression for y1b.

mylogistic = smf.glm(formula = 'yb ~ x1b + x2 + x3 + x4 + x5', data = df,
                     family = sm.families.Binomial())
mylfit = mylogistic.fit()
mylfit.summary()
Generalized Linear Model Regression Results
Dep. Variable: yb No. Observations: 200
Model: GLM Df Residuals: 194
Model Family: Binomial Df Model: 5
Link Function: Logit Scale: 1.0000
Method: IRLS Log-Likelihood: -30.654
Date: Fri, 29 Jul 2022 Deviance: 61.307
Time: 22:53:00 Pearson chi2: 217.
No. Iterations: 7 Pseudo R-squ. (CS): 0.05871
Covariance Type: nonrobust
coef std err z P>|z| [0.025 0.975]
Intercept -0.4354 1.309 -0.333 0.739 -3.002 2.131
x1b 1.2721 0.845 1.505 0.132 -0.384 2.928
x2 2.6897 1.418 1.897 0.058 -0.089 5.469
x3 -0.0537 1.270 -0.042 0.966 -2.542 2.435
x4 2.6576 1.438 1.848 0.065 -0.160 5.476
x5 1.8752 1.330 1.409 0.159 -0.732 4.483

If we treat y1b as count data, a Poisson regression can be fitted.

myPois = smf.glm(formula = 'yb ~ x1b + x2 + x3 + x4 + x5', data = df,
                 family = sm.families.Poisson())
mypfit = myPois.fit()
mypfit.summary()
Generalized Linear Model Regression Results
Dep. Variable: yb No. Observations: 200
Model: GLM Df Residuals: 194
Model Family: Poisson Df Model: 5
Link Function: Log Scale: 1.0000
Method: IRLS Log-Likelihood: -199.55
Date: Fri, 29 Jul 2022 Deviance: 17.091
Time: 22:53:00 Pearson chi2: 8.99
No. Iterations: 4 Pseudo R-squ. (CS): 0.002487
Covariance Type: nonrobust
coef std err z P>|z| [0.025 0.975]
Intercept -0.2045 0.288 -0.710 0.477 -0.769 0.360
x1b 0.0445 0.146 0.304 0.761 -0.242 0.331
x2 0.0965 0.249 0.387 0.699 -0.392 0.585
x3 -0.0088 0.254 -0.035 0.972 -0.507 0.490
x4 0.1072 0.267 0.402 0.688 -0.416 0.630
x5 0.0750 0.253 0.296 0.767 -0.421 0.571

previous

9.2. Hypothesis Tests

next

9.5. Generalized Additive Models